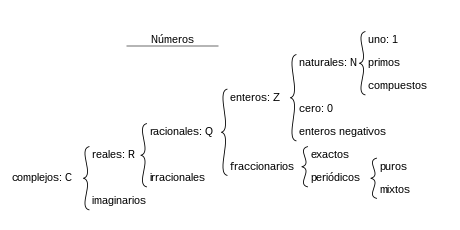
Los números
complejos son una extensión de los números
reales, es decir, los números reales forman parte de los números complejos.
El conjunto de los números complejos se
designa como C,
siendo R el conjunto de los reales se cumple que R es subconjunto de C.
Los números complejos incluyen todas las raíces de los polinomios,
a diferencia de los reales.
En la historia de las matemáticas a través del tiempo, los números complejos son la herramienta de trabajo del álgebra, del análisis, así como de ramas de las matemáticas puras y aplicadas como variable compleja, ecuaciones diferenciales, aerodinámica y electromagnetismo entre otras de gran importancia. Además los números complejos se utilizan en muchos campos de la física (como en la mecánica cuántica) y en ingeniería, (como en la electrónica y las telecomunicaciones, por su utilidad para representar las ondas electromagnéticas y la corriente eléctrica).
Investigar:
1.Asociación de la Ingeniería Electrónica
con el Análisis de Fourier.
2.Asociación de la Mecánica Cuántica con
los Espacios de Hilbert.

A primera vista, parece que el problema de analizar formas de ondas complejas representa una tarea formidable. Sin embargo, si la forma de la onda es periódica, se puede representar con una precisión arbitraria, mediante la superposición de un número suficientemente grande de ondas senoidales que forman una serie armónica.
ResponderEliminarToda función f(t) periódica de periodo P, se puede representar en forma de una suma infinita de funciones armónicas, es decir,
El propósito de este artículo es analizar la estructura y la ontología de los espacios de Hilbert de la Mecánica Cuántica. Se argumenta contra el realismo estructural el hecho de que los modelos matemáticos no representan la estructura del Mundo. Además, la estructura matemática no se conserva a través del cambio de teorías científicas, como demuestra la historia de los espacios de Hilbert
ResponderEliminarAsociación de la Ingeniería Electrónica con el Análisis de Fourier.
ResponderEliminarEn electrónica se asocia en la teoría de señales ya que estas sirven mucho en el procesamiento digital de señales, la cual se ha desarrollado rápidamente en los últimos 30 años. Este rápido desarrollo es resultado de avances tecnológicos tanto en los ordenadores digitales como en la fabricación de circuitos integrados. El procesamiento de señales se correlaciona con las series de Fourier ya que esta nos permite expresar una función periódica de tiempo como la suma de un número infinito de senoides cuyas frecuencias están armónicamente relacionadas esto radica en que la serie de Fourier facilita el arduo trabajo del manejo con señales, ya que para que nosotros podamos procesar estas señales es necesario expresarlas como una combinación lineal de términos, lo cual nos lo proporciona la serie de Fourier.
Asociación de la Mecánica Cuántica con los Espacios de Hilbert.
ResponderEliminarEl espacio de Hilbert es un espacio vectorial infinitamente grande su trabajo sobre ecuaciones integrales llevado a cabo en 1912 David Hilbert tuvo la visión de tener que postular un espacio vectorial infinitamente grande para poder proyectar todo el aparato matemático de la Mecánica Cuántica sobre una base rigurosamente formal. Propuso también que los componentes de los “vectores” pudiesen ser números imaginarios o números complejos sin estar limitados a ser números reales, redefiniendo a la vez el concepto del producto interno de dos vectores para que dicho producto pudiese seguir siendo un número real con significado físico.
Asociación de la Mecánica Cuántica con los Espacios de Hilbert.
ResponderEliminarEl espacio de Hilbert es un espacio vectorial infinitamente grande. En su momento, esto fue una idea revolucionaria, en virtud de que todos los espacios vectoriales, inclusive los espacios matemáticos abstractos, eran finitos. Pero afortunadamente en su trabajo sobre ecuaciones integrales llevado a cabo en 1912 David Hilbert tuvo la visión suficiente para captar la necesidad de tener que postular un espacio vectorial infinitamente grande para poder proyectar todo el aparato matemático de la Mecánica Cuántica sobre una base rigurosamente formal. Y quince años después correspondió a otro matemático igualmente brillante, el matemático húngaro John von Neumann, el darle en 1927 una definición axiomática al espacio vectorial de Hilbert en su ya famosa obra Mathematische Grundlagen der Quantenmechanik. Pero Hilbert no solo propuso un espacio vectorial infinitamente grande. Propuso también que los componentes de los “vectores” pudiesen ser números imaginarios o números complejos sin estar limitados a ser números reales, redefiniendo a la vez el concepto del producto interno de dos vectores para que dicho producto pudiese seguir siendo un número real con significado físico.
En matemáticas, una serie de Fourier descompone funciones periódicas o señales periódicas en la suma de funciones oscilantes simples, como senos y cosenos (o exponentials complejos). El estudio de la serie de Fourier Es una rama del análisis de Fourier.
ResponderEliminarLa serie de Fourier Se nombra en honor de Jean-Baptiste José Fourier (1768-1830), que hizo contribuciones importantes al estudio de la serie trigonométrica, después de investigaciones preliminares por Leonhard Euler y Daniel Bernoulli. Fourier introdujo la serie con el fin de solucionar la ecuación del calor en una placa de metal.
En las ramas de la Electrónica e Ingeniería se trabajan diferentes formas de señales tales como: sinusoidal, cuadrada y triangular. Todas estas señales mencionadas son periódicas ósea que se repiten luego de un tiempo. La aplicación del osciloscopio nos permite entender un poco mejor como son estas señales que se pueden determinar calculando la Serie de Fourier para cada una de estas.
Este comentario ha sido eliminado por el autor.
ResponderEliminarAsociación de la Ingeniería Electrónica con el Análisis de Fourier.
ResponderEliminarEste denota la perpendicularidad entre dos elementos, es decir, dos calles que se cruzan en un ángulo recto presentan una configuración ortogonal, Además de las conocidas señales periódicas seno y coseno, se emplea una gran cantidad de formas de onda periódicas para simular señales físicas, tales como señales rectangulares, diente de sierra, señales rectificadas, señales moduladas, entre otros, que se pueden representar en el dominio de la frecuencia por ello es usada en muchas ingenierías como en la electrónica, mecánica, y otras más gracias a la aplicación de la misma en la electrónica y mecánica se ha experimentado una gran avance notable ya que favorece de forma relevante la innovación en los avances tecnológicos . Dicho análisis se la logrado esparcir y de una manera apreciable, es usada para muchas cosas en la ingeniería, facilitando así algún trabajo específico, Las series de Fourier constituyen la herramienta matemática básica del análisis para estudiar funciones periódicas a través de la descomposición de dicha función en una suma infinita de funciones.
Vale destacar que en la ingeniería mecánica es muy usada para obtener soluciones prácticas, en la teoría de la transmisión del calor.
Asociación de la Mecánica Cuántica con los Espacios de Hilbert.
ResponderEliminarel concepto de espacio de Hilbert es una generalización del concepto de espacio euclídeo. Esta generalización permite que nociones y técnicas algebraicas y geométricas aplicables a espacios de dimensión dos y tres se extiendan a espacios de dimensión arbitraria, incluyendo a espacios de dimensión infinita. Espacios de Hilbert Es un espacio lineal de vectores dotado de producto escalar, que es completo en la topología derivada de dicho producto escalar.
Este comentario ha sido eliminado por el autor.
ResponderEliminarAsociación de la Ingeniería Electrónica con el Análisis de Fourier.
EliminarSe puede decir que Fourier emplea una gran variedad de formas de onda periódicas para simular señales físicas, tales como señales rectangulares, señales rectificadas, señales moduladas, entre otras; que se pueden representar en la frecuencia por ello es usada en muchas ingenierías tales como en la electrónica y mecánica que son las mas empleadas en este caso, por otra parte se ha experimentado un gran avance en los últimos 30 años gracias a dicho avance se a logrado esparcir de una manera apreciable para muchas cosas en la ingeniería facilitando así algunos trabajos en específicos. A su ves el procesamiento de señales se correlacionan con las series de Fourier ya que esta nos permite expresar una función periódica de tiempo como la suma de un número infinito de senoides cuyas frecuencias son armónicas y para que nosotros podamos procesar estas señales es necesario expresarlas como una combinación lineal de términos, lo cual nos lo proporciona la serie de Fourier.
Asociación de la Mecánica Cuántica con los Espacios de Hilbert
ResponderEliminarEn esta ocasión la mecánica cuántica con los espacios de Hilbert es una generalización que nos permite técnicas algebraicas y geométricas aplicables a espacios de (2) y (3) dimensiones arbitraria incluyendo espacios de dimensión infinita.En su momento, esto fue una idea revolucionaria, en virtud de que todos los espacios vectoriales inclusive los espacios matemáticos eran finitos, pero afortunadamente en su trabajo sobre ecuaciones integrales, llevado a cabo en 1912 David Hilbert tuvo la visión suficiente para captar la necesidad de tener que postular un espacio vectorial infinitamente grande para poder proyectar todo el aparato matemático de la Mecánica Cuántica sobre una base rigurosamente formal. Luego de 15años después John von Neumann seria quien se en cargara de fortalecerte la teoría de David Hilbert pero Hilbert no solo propuso un espacio vectorial infinitamente grande, también propuso que los componentes de los (vectores) pudiesen ser números imaginarios o números complejos sin estar limitados a ser números reales.
ResponderEliminar1. Asociación de la Ingeniería Electrónica con el Análisis de Fourier.
Se puede decir que Fourier emplea una gran variedad de formas de onda periódicas para simular señales físicas, tales como señales rectangulares, señales rectificadas, señales moduladas, entre otras; que se pueden representar en la frecuencia por ello es usada en muchas ingenierías tales como en la electrónica y mecánica que son las mas empleadas en este caso, por otra parte se ha experimentado un gran avance en los últimos 30 años gracias a dicho avance se a logrado esparcir de una manera apreciable para muchas cosas en la ingeniería facilitando así algunos trabajos en específicos. A su ves el procesamiento de señales se correlacionan con las series de Fourier ya que esta nos permite expresar una función periódica de tiempo como la suma de un número infinito de senoides cuyas frecuencias son armónicas y para que nosotros podamos procesar estas señales es necesario expresarlas como una combinación lineal de términos, lo cual nos lo proporciona la serie de Fourier.
2. Asociación de la Mecánica Cuántica con los Espacios de Hilbert
Es una generalización del concepto de espacio euclídeo. Esta generalización permite que nociones y técnicas algebraicas y geométricas aplicables a espacios de dimensión dos y tres se extiendan a espacios de dimensión arbitraria, incluyendo a espacios de dimensión infinita. Ejemplos de tales nociones y técnicas son la de ángulo entre vectores, ortogonalidad de vectores, el teorema de Pitágoras, proyección ortogonal, distancia entre vectores y convergencia de una sucesión. El nombre dado a estos espacios es en honor al matemático David Hilbert quien los utilizó en su estudio de las ecuaciones integrales.
Mas formalmente, se define como un espacio de producto interior que es completo con respecto a la norma vectorial definida por el producto interior. Los espacios de Hilbert sirven para clarificar y para generalizar el concepto de series de Fourier, ciertas transformaciones lineales tales como la transformación de Fourier, y son de importancia crucial en la formulación matemática de la mecánica cuántica.
David Berroteran
CI.:26.470.437
ING-M-4S-D-01
Asociación de la Ingeniería Electrónica con el Análisis de Fourier.
ResponderEliminarEn ingeniería electrónica se asocia en la teoría de señales ya que estas sirven mucho en el procesamiento digital de señales, y en los resultado de avances tecnológicos tanto en los ordenadores digitales como en la fabricación de circuitos integrados, el analizáis de Fourier facilita el arduo trabajo del manejo con señales, ya que para que nosotros podamos procesar estas señales es necesario expresarlas como una combinación lineal de términos; también es importante que las series de Fourier constituyen la herramienta matemática básica del análisis para estudiar funciones periódicas a través de la descomposición de dicha función en una suma infinita de funciones.
Vale destacar que en la ingeniería mecánica es muy usada para obtener soluciones prácticas, en la teoría de la transmisión del calor.
Asociación de la Mecánica Cuántica con los Espacios de Hilbert
Esta asociación permite que nociones y técnicas algebraicas y geométricas aplicables a espacios de segunda y tercera dimensiones se extiendan a espacios de dimensiones arbitrarias, incluyendo a espacios de dimensión infinita, esto fue debido al estudio de las ecuaciones integrales que realizo el matemático David Hilbert que aporto gracias a su teoría y tuvo la visión suficiente para captar la necesidad de tener que postular un espacio vectorial, infinitamente grande para poder proyectar todo el aparato matemático de la Mecánica Cuántica sobre una base rigurosamente formal.
También propuso que los componentes de los (vectores) pudiesen ser números imaginarios o números complejos sin estar limitados a ser números reales.
Angel Viera
CI:25736175
Ingeniería Mecánica 4S.
Asociación de la Ingeniería Electrónica con el Análisis de Fourier.
ResponderEliminarEn electrónica se asocia en la teoría de señales ya que estas sirven mucho en el procesamiento digital de señales, la cual se ha desarrollado rápidamente en los últimos 30 años. Este rápido desarrollo es resultado de avances tecnológicos tanto en los ordenadores digitales como en la fabricación de circuitos integrados. El procesamiento de señales se correlaciona con las series de Fourier ya que esta nos permite expresar una función periódica de tiempo como la suma de un número infinito de senoides cuyas frecuencias están armónicamente relacionadas esto radica en que la serie de Fourier facilita el arduo trabajo del manejo con señales, ya que para que nosotros podamos procesar estas señales es necesario expresarlas como una combinación lineal de términos, lo cual nos lo proporciona la serie de Fourier.
Asociación de la Mecánica Cuántica con los Espacios de Hilbert.
El espacio de Hilbert es un espacio vectorial infinitamente grande. En su momento, esto fue una idea revolucionaria, en virtud de que todos los espacios vectoriales, inclusive los espacios matemáticos abstractos, eran finitos. Pero afortunadamente en su trabajo sobre ecuaciones integrales llevado a cabo en 1912 David Hilbert tuvo la visión suficiente para captar la necesidad de tener que postular un espacio vectorial infinitamente grande para poder proyectar todo el aparato matemático de la Mecánica Cuántica sobre una base rigurosamente formal. Y quince años después correspondió a otro matemático igualmente brillante, el matemático húngaro John von Neumann, el darle en 1927 una definición axiomática al espacio vectorial de Hilbert en su ya famosa obra Mathematische Grundlagen der Quantenmechanik. Pero Hilbert no solo propuso un espacio vectorial infinitamente grande. Propuso también que los componentes de los “vectores” pudiesen ser números imaginarios o números complejos sin estar limitados a ser números reales, redefiniendo a la vez el concepto del producto interno de dos vectores para que dicho producto pudiese seguir siendo un número real con significado físico.
LUIS VILLAMIZAR
C.I.: 25 674 843
ING. MECANICA
Asociación de la Ingeniería Electrónica con el Análisis de Fourier.
ResponderEliminarEs muy utilizada en ingeniería electrónica y eléctrica, ya que las señales o formas de onda, ocupan un
lugar importante a la hora de diseñar y analizar circuitos. La Transformada de Fourier permite
representar una señal continua de periodo infinito en el dominio de la frecuencia. Mediante la
Transformada de Fourier se puede determinar la amplitud y la frecuencia de las señales sinusoidales
en que se puede descomponer una señal continua. Se utiliza para analizar los cambios que ocurren
cuando las señales viajan a traves de un medio de transmision, diseñar sistemas para compensar la
distorsion de las señales en los sistemas de transmision, diseñar supresores y canceladores de ecos en
lineas telefonicas, compactar señales de audio (mp3 y mp4), producir efectos de sonidos, filtrar
imagenes, compactar imagenes, entre otras. El analisis de Fourier ha hecho posible que actualmente
tengamos muchos dispositivos tecnologicos que hacen nuestras vidas mas comodas.
Asociación de la Mecánica Cuántica con los Espacios de Hilbert.
Todos los espacios finito-dimensionales con producto interior son espacios de Hilbert. Los elementos de
un espacio de Hilbert abstracto a veces se llaman "vectores". Es aplicado típicamente en sucesiones de
números complejos o de funciones y Formulaciones matemáticas de la mecánica cuántica. En mecánica
cuántica por ejemplo, un conjunto físico es descrito por un espacio complejo de Hilbert que contenga las
"funciones de ondas" para los estados posibles del conjunto. En 1912, esto fue una idea unica, en virtud
de que todos los espacios vectoriales, inclusive los espacios matemáticos abstractos, eran finitos. Pero
Hilbert no solo propuso un espacio vectorial infinitamente grande. Propuso también que los
componentes de los “vectores” pudiesen ser números imaginarios o números complejos sin estar
limitados a ser números reales, redefiniendo a la vez el concepto del producto interno de dos vectores
para que dicho producto pudiese seguir siendo un número real con significado físico.
Ing. Mecanica
Integrantes:
· Orwell Silva
· Dylan Servita
Los números complejos son la herramienta de trabajo del álgebra, análisis, así como de ramas de las matemáticas puras y aplicadas como variable compleja, ecuaciones diferenciales, facilita el cálculo de integrales, en aerodinámica, hidrodinámica y electromagnetismo entre otras de gran importancia. Además, los números complejos se utilizan por doquier en matemáticas, en muchos campos de la física (notoriamente en la mecánica cuántica) y en ingeniería, especialmente en la electrónica y las telecomunicaciones, por su utilidad para representar las ondas electromagnéticas y la eléctrica. En matemáticas, estos números constituyen un cuerpo y, en general, se consideran como puntos del plano
ResponderEliminarSe define cada número complejo z como un par ordenado de números reales z = (a, b). A su
Vez el primer elemento a se define como parte real de z, el segundo elemento b se define como parte imaginaria de z, Luego en el conjunto ℂ de los números complejos, se definen tres operaciones y la relación de igualdad