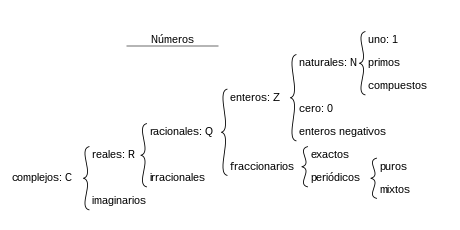
Los Números Complejos

Los números complejos son una extensión de los números reales, es decir, los números reales forman parte de los números complejos.  El conjunto de los números complejos se designa como C, siendo R  el conjunto de los reales se cumple que  R  es subconjunto de C. Los números complejos incluyen todas las raíces de los polinomios, a diferencia de los reales.

Todo número complejo puede representarse como la suma de un número real y un número imaginario (que se indica con la letra i).

En la historia de las matemáticas a través del tiempo, los números complejos son la herramienta de trabajo del álgebra, del análisis, así como de ramas de las matemáticas puras y aplicadas como variable compleja, ecuaciones diferenciales, aerodinámica y electromagnetismo entre otras de gran importancia. Además los números complejos se utilizan en muchos campos de la física (como en la mecánica cuántica) y en ingeniería, (como en la electrónica y las telecomunicaciones, por su utilidad para representar las ondas electromagnéticas y la corriente eléctrica).

Investigar:

1.Asociación de la Ingeniería Electrónica con el Análisis de Fourier.

2.Asociación de la Mecánica Cuántica con los Espacios de Hilbert.

Historia de los Números Complejos

La primera referencia conocida a raíces cuadradas de números negativos proviene del trabajo de los matemáticos griegos, como Herón de Alejandría en el siglo I antes de Cristo, como resultado de una imposible sección de una pirámide. Los complejos se hicieron más patentes en el Siglo XVI, cuando la búsqueda de fórmulas que dieran las raíces exactas de los polinomios de grados 2 y 3 fueron encontradas por matemáticos italianos como Tartaglia, Cardano.

Aunque sólo estaban interesados en las raíces reales de este tipo de ecuaciones, se encontraban con la necesidad de lidiar con raíces de números negativos. El término imaginario para estas cantidades fue acuñado por Descartes en el Siglo XVII y está en desuso. La existencia de números complejos no fue completamente aceptada hasta la más abajo mencionada interpretación geométrica que fue descrita por Wessel en 1799, redescubierta algunos años después y popularizada por Gauss. La implementación más formal, con pares de números reales fue dada en el Siglo XIX.

 

El primero en usar los números complejos fue el matemático italiano Girolamo Cardano (1501–1576) quien los usó en la fórmula para resolver las ecuaciones cúbicas. El término “número complejo” fue introducido por el gran matemático alemán Carl Friedrich Gauss (1777–1855) cuyo trabajo fue de importancia básica en álgebra, teoría de los números, ecuaciones diferenciales, geometría diferencial, geometría no euclídea, análisis complejo, análisis numérico y mecánica teórica, también abrió el camino para el uso general y sistemático de los números complejos.

Investigar:

1.Biografías de Girolamo Cardano y Carl Friedrich Gauss.

2. Relación de Caspar Wessel (1745-1818) con los números complejos.